Kotlinで最初に迷ったのがべき乗。例えばPythonで3の3乗を行うにはこのように記述します。
3 ** 3
しかし残念ながらKotlinではこの演算子が使えません。今回はこのべき乗を行う方法と、数学的演算を行うKotlin.Mathパッケージのプロパティ/メソッドをまとめてお送りします。
べき乗を行うには
JavaのMathモジュールを使う
Kotlinでべき乗を行う簡単な方法は2つ。1つはJavaのMathモジュールの静的メソッドpowです。
Math.pow(3.0,3.0) //27.0
Mathモジュールはインポート無しで扱うことができますが、引数はDouble型でなければなりません。
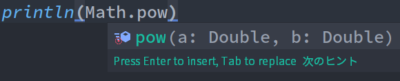
Double型でない可能性がある場合は明示的に変換しておきましょう。
val x = 3
Math.pow(x.toDouble(),3.0)
「pow」は「power」の略:
- raise to the second power (2乗する)
- 2 to the 4th power is 16. (2の4乗は16)
プログレッシブ英和中辞典(第４版)
KotlinのMathパッケージをインポートする
もう1つはKotlinのMathパッケージ。こちらもメソッド名はpow。importして使用します。
import kotlin.math.*
fun main() {
println(3.0.pow(3)) //3.0の3乗
}
//27.0
この場合は呼び出し元の型がDoubleかFloat、引数はInt/Double/Floatのどれかである必要があります。
Mathパッケージ
kotlin.Mathパッケージにはこれ以外にも、様々な数学的計算を行うためのプロパティやメソッドが含まれています。
ここでは2020年4月現在でのMathパッケージのプロパティ/メソッドの全てを記載しています。それぞれのメソッドについて詳しく知りたい方はKotlin公式ドキュメント(英語)をご覧ください。
kotlin.math - Kotlin Programming Language
kotlinlang.org
プロパティ
| 名称 | 意味 | 例 |
|---|---|---|
| x.absoluteValue | 絶対値を返す | (-92.382).absoluteValue == 92.382 |
| E | ネイピア数(e) | E == 2.718281828459045 |
| PI | π | PI == 3.141592653589793 |
| x.sign | 正/負/0の判定 | -30.sign == -1 0.sign == 0 30.sign == 1 |
| x.ulp | ULP(Unit in the Last Place) | PI.ulp == 4.440892098500626E-16 |
参考文献
https://ja.wikipedia.org/wiki/%E3%83%8D%E3%82%A4%E3%83%94%E3%82%A2%E6%95%B0
ULPについては以下を参照。
機械イプシロン - PukiWiki
tessy.org
[Java][Scala] 浮動小数点の有効桁数と同値性
浮動小数点で掛け算や割り算を行うと微妙に正確な値からずれていって困っちゃいますよね。例えば、いろいろ計算した結果、机上ではぴったり１になるはずなのに、コンピュータ上では、0.9999999になってたりとか。こんなとき困るのが同値性を検証するときです。こっちは１だと思ってるので、...
cheetahs-blog.blogspot.com
正負/小数点のメソッド
| 名称 | 意味 | 例 |
|---|---|---|
| abs(x) | 絶対値を返す | abs(-5) == 5 |
| sign(x) | 正/負/0の判定 | sign(8) == 1.0 sign(-8.0) == -1.0 |
| x.withSign(s) | xにsの±を適用 | 9.0.withSign(-80) == -9.0 9.0.withSign(80) == 9.0 |
| ceil(x) | 小数点以下を切り上げ | ceil(3.141) == 4 |
| floor(x) | 小数点以下を切り捨て (x以下で最大の整数) | floor(-5.871) == -6.0 |
| truncate(x) | 小数点以下を切り捨て (xから0に最も近い整数) | truncate(-5.871) == -5.0 |
| round(x) | 小数点以下を四捨五入 | round(5.8) == 6.0 |
| x.roundToInt() | 四捨五入してIntに変換 | 3.38.roundToInt() == 3 |
| x.roundToLong() | 四捨五入してLongに変換 | 3.38.roundToLong() == 3 |
比較/剰余のメソッド
| 名称 | 意味 | 例 |
|---|---|---|
| max(a,b) | a,b2つの最大値 | max(3,-8) == 3 |
| min(a,b) | a,b2つの最小値 | min(-5,-2) == -5 |
| x.IEEErem(y) | xをyで割った剰余(IEEE754標準方式) |
参考文献
IEEE754について。
浮動小数点数について本気出して考えてみた - 一から勉強させてください
（2016/12/30 追記）コメントでご指摘頂いた箇所に関して修正しました。 この前たまたまこちらの記事を見つけて、浮動小数点数について全然理解してないなって思ったので勉強してみました。 前提 コンピュータの中に保存されているデータはすべて 0 と 1 の集まり（ビット列）で表現されている。そしてどういうビット列をど...
dangerous-animal141.hatenablog.com
指数/対数(log)/平方根のメソッド
| 名称 | 意味 | 例 |
|---|---|---|
| x.pow(y) | xをy乗する | 5.0.pow(8) == 390625.0 |
| exp(x) | ネイピア数のx乗 | exp(3.0) == 20.085… |
| expm1(x) | expの結果-1 | |
| log(m,x) | logxm | log(55.0,2.0) == 5.7813… |
| log2(m) | log2m | log2(8.0) == 3.0 |
| log10(m) | log10m | log10(100.0) == 2.0 |
| ln(m) | logem | ln(3.0) == 1.098612… |
| ln1p(m) | loge(m+1) | ln1p(3.0) == 1.386294… |
| sqrt(x) | xの正の平方根 | sqrt(9.0) == 3.0 |
| hypot(x,y) | sqrt(x2+y2) |
浮動小数点数のメソッド
| 名称 | 意味 | 例 |
|---|---|---|
| x.nextDown() | x未満で最も近い浮動小数点数 | 5.2.nextDown() == 5.1999… |
| x.nextUp() | x超過で最も近い浮動小数点数 | 5.2.nextUp() == 5.2000…1 |
| x.nextTowards(y) | x超過y未満で、xに最も近い浮動小数点数 |
三角関数のメソッド
| 名称 | 意味 |
|---|---|
| sin(x) | rad = xのときの正弦 |
| cos(x) | rad = xのときの余弦 |
| tan(x) | rad = xのときの正接 |
| asin(x) | xの逆正弦をradで返す |
| acos(x) | xの逆余弦をradで返す |
| atan(x) | xの逆正接をradで返す |
| atan2(y,x) | atan(y / x)をradで返す |
参考文献
三角関数の基礎。
三角関数のsin・cos・tanとは？使い方・求め方・覚え方を図表で解説！｜高校生向け受験応援メディア「受験のミカタ」
sin(サイン)・cos(コサイン)・tan(タンジェント)について、三角関数が苦手な方でも理解できるよう、見やすい図を使いながら丁寧に解説しています。その求め方や覚え方、重要な公式、さらに文末には練習問題も用意しているので活用してみてください。
juken-mikata.net
逆三角関数について。
逆三角関数 - 基礎からの数学入門
中学生程度の内容から大学の初級程度の数学をわかりやすく解説。問題を解きながら理解して、数学を使えるようになることを目指します。
math.keicode.com
双曲線関数のメソッド
| 名称 | 意味 |
|---|---|
| asinh(x) | xの逆双曲線正弦 |
| acosh(x) | xの逆双曲線余弦 |
| atanh(x) | xの逆双曲線正接 |
| sinh(x) | xの双曲線正弦 |
| cosh(x) | xの双曲線余弦 |
| tanh(x) | xの双曲線正接 |
参考文献
双曲線関数について。
https://www.geisya.or.jp/~mwm48961/electro/hyperbolic_fun1.htm
www.geisya.or.jp