Pythonコンテナ型、最後はset(集合)です。set型はリストやタプル、辞書とは違う大きな特徴を持っています。
set型の新規作成
まずはset型を作成していきます。
a = {1,2,3} #{1, 2, 3}
b = set() #set()値を含んだsetを新規作成するには波括弧{}で要素を囲みます。
値を含まない空のsetの場合は2行目のように「set()」で作成します。中身の無い波括弧{}だけだと空の辞書になってしまうので注意しましょう。
set型の基本操作
setはインデックス番号やキーが無いため、簡単に個別の値にアクセスする方法はありません。しかし要素を追加したり削除することはリストと同じようにできます。
要素を追加する
a = {1,2,3}
a.add(4) #{1, 2, 3, 4}
a.update([5,6]) #{1, 2, 3, 4, 5, 6}要素を追加するにはaddメソッドかupdateメソッドを使います。単体の値であればadd、複数の値を含むリストやタプル、セットなどのイテラブルな値であればupdateを使用しましょう。
a.update("hello") #{1, 2, 3, 'l', 'h', 'e', 'o'}文字列はイテラブルなので、そのままupdateメソッドに入れると1文字ずつに分解されます。
要素を削除する
a = {1,2,3,4,5}
print(a.pop()) #1
a.remove(3)
print(a) #{2, 4, 5}pop、removeメソッドで要素を削除することができます。setの場合、popメソッドで削除されるのはランダムな値であることには注意しましょう。
a = {1,2,3,4,5}
a.discard(3) #{1, 2, 4, 5}discardメソッドも値を指定して削除できます。removeメソッドは存在しない値を指定してしまった場合エラーになりますが、discardメソッドはエラーにはならず、削除という行為自体が無視されます。
a = {1,2,3,4,5}
a.clear() #set()リストと同じように、clearメソッドで要素全てを削除できます。
set型の特徴
ここからはset型の特徴を見ていきます。
a = {1,2,3,1,2,3}
b = {"PHP","Java","Python"}
print(a) #{1, 2, 3}
print(b) #{'Java', 'PHP', 'Python'}上のコード1行目では同じ数値が2回繰り返されていますが、実際に作成されたset型の要素は各々1つずつしかありません。
さらに2行目、作成時にPHP→Java→Pythonと入れたはずですが、出力時にはこの順番が無視されています。
このようにset型には、
- 重複した値は入らない
- 要素の順番を保持しない
という大きな特徴があります。
リストや辞書との違い
ここで今までのコンテナ型と合わせて、set型がどのように要素を管理しているのかを確認してみましょう。
まずはリストとタプルです。
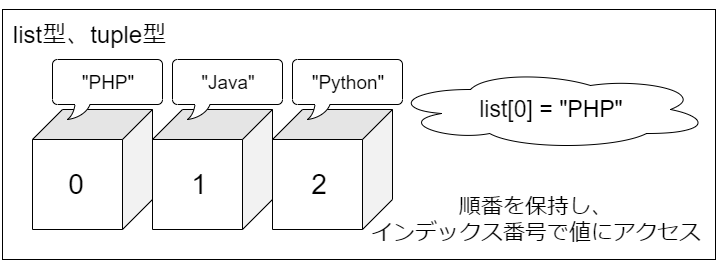
リストとタプルは整然と並んだ箱に要素を入れているようなイメージ。箱には通し番号が付いていて、要素を取り出すときは箱の番号を指定して中にある値を取り出します。
続いて辞書です。
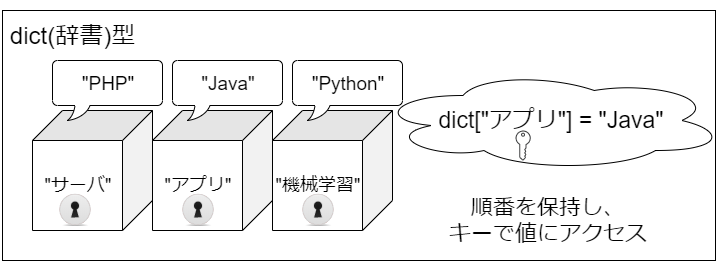
辞書も箱が並んでいるのは同じですが、箱の名前は開発者によって決められます。個別の値にアクセスするには箱の名前をキーとして、そのキーで箱を開けて中身を取り出します。
元々は順番が保持されていなかった辞書型も、Python3.7以降は順番を保持することが保証されました。
ではsetはどうでしょう。
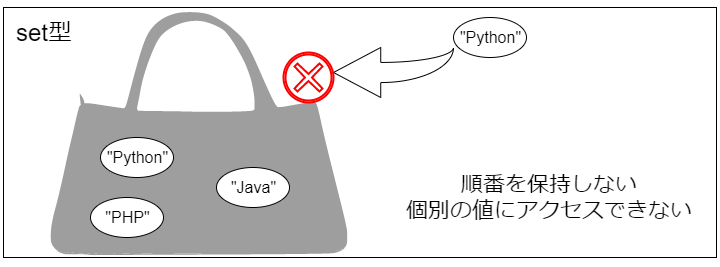
setは例えばトートバッグの中に値をポンポンと入れているようなイメージ。バッグの中身に順番はありません。
インデックス番号もキーも無いので、個別の値にアクセスすることができません。しかも2つ以上同じものを入れようとすると、エラーにはなりませんが無視されてしまいます。
こう聞くと少々特殊でクセが強い型にも思えますが、setにはsetにしかできないことがあります。それが集合演算です。
集合演算
setによって括られた要素は、全体で1つの「集合」とみなすことができます。集合とは簡単に言えば「ものの集まり」です。例えば学校や会社、スポーツのチームなどは、それを構成する人々をまとめた集合と言えます。
集合は他の集合と合わせたり比較したりすることで、新たな集合を生み出すことができます。代表的なものに
- 和集合
- 積集合
- 差集合
- 対称差集合
があり、これらをひとまとめにして集合演算と呼びます。
多少数学的な話も入ってきますが、ここでご紹介するのは誰にでも理解しやすい話なので、少々長くなりますがお付き合いください。
和集合
集合演算の中で最も単純なのが和集合です。順を追って説明していきましょう。
① まず2つの異なる集合を用意します。
コードで表現するとこのような感じです。setを2つ作成しました。
a = {1,2,3,4,5}
b = {3,4,5,6,7}② このAとBを足し合わせて、新たなCという集合を作ります。集合の中には重複したものは不要なので、値がダブって2つ以上になったら1つを残してゴミ箱へ捨ててしまいましょう。
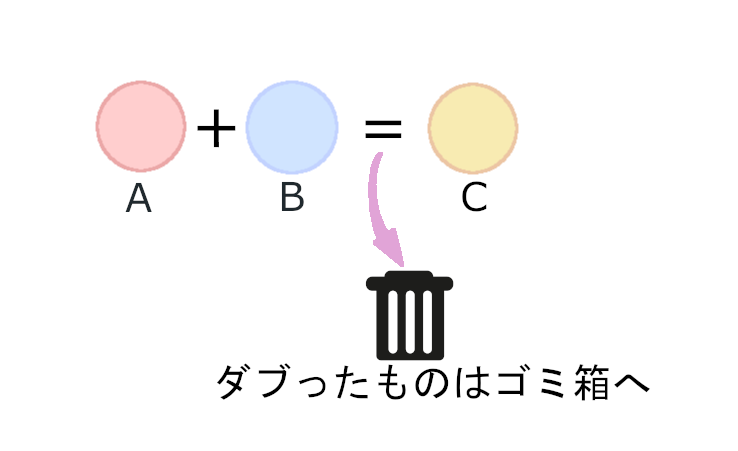
c = a | bこれをPythonで記述するとこのような形になります。集合同士を足し合わせるのには、set同士を「|」(パイプ記号)でつなぎます。そうすると、
print(c) #{1, 2, 3, 4, 5, 6, 7}AとBを足し合わせ、さらに値が重複しない新たな集合ができました。これが和集合です。
ちなみに演算子の代わりに、unionメソッドでも同様の結果が得られます。
c = a.union(b)少しだけ数学的な説明を付け加えましょう。この新しくできたCは、AとB両方の値を全て含んでいます。当然ですね。
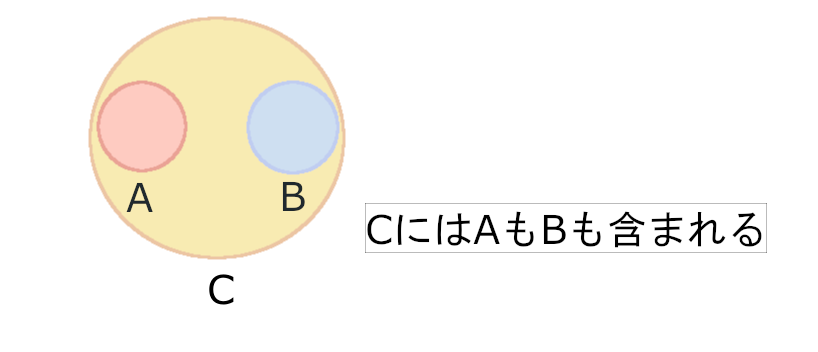
このとき、CをAとBの上位集合、AとBをCの部分集合と呼びます。
部分集合かどうかを調べる
別の演算子やset型のメソッドを使って、ある集合が別の集合の部分集合かどうかを調べることができます。
a = {1,2,3,4,5}
b = {3,4,5,6,7}
c = a | b
print(a <= c) #True
print(c.issubset(b)) #False演算子は「<=」、メソッドはissubsetを使用します。下の2行ではまず演算子を使用し、「aはcの部分集合であるか」を調べ、メソッドを使用して「cはbの部分集合であるか」を調べています。
上位集合かどうかを調べる
同じように、ある集合が別の集合の上位集合であるかどうかを調べてみましょう。
print(a >= c) #False
print(c.issuperset(b)) #Trueこの場合演算子は先ほどと逆、「>=」で「aはcの上位集合であるか」、issupersetメソッドで「cはbの上位集合であるか」を調べています。
積集合
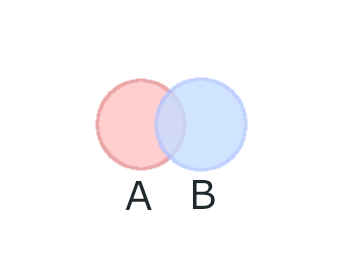
続いて積集合です。再び2つの集合を用意します。

このAとBの中に入っている要素には、AにもBにも含まれている値(要素)があると仮定しましょう。
その状況を図に表すとこんな風になります。
この重なり合った部分だけを抜き出せば、AにもBにも含まれる値だけが取り出せます。これを新しい集合としましょうというのが積集合です。
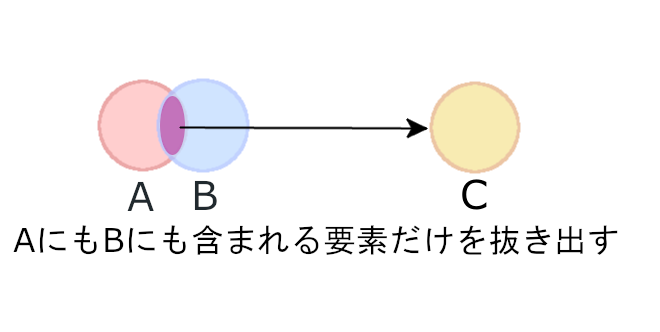
ではこれをPythonで記述してみます。
a = {1,2,3,4,5}
b = {3,4,5,6,7}
c = a & b
print(c) #{3, 4, 5}積集合の場合は「&」(アンド記号orアンパサンド)を演算子として使用します。a,bに共通する値3,4,5が抜き出され、新たな集合が出来上がりました。
&演算子の代わりに、intersectionメソッドを使用してもかまいません。結果は同じです。
c = a.intersection(b)差集合
差集合は途中まで積集合と同じです。

2つの集合にはどちらにも入っている値があるとします。
ここから「Aにのみ」入っている値を取り出して、新しい集合を作ります。Bにも入っている値は不要です。
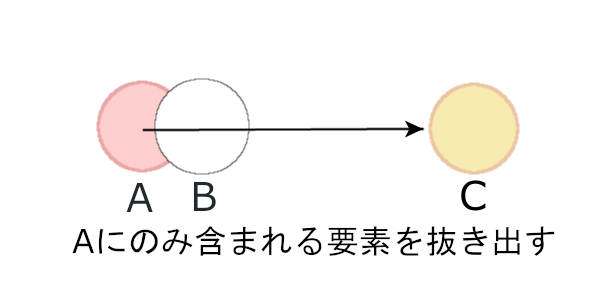
これが差集合です。Pythonではこの差集合をこのように記述します。
a = {1,2,3,4,5}
b = {3,4,5,6,7}
c = a - b
print(c) #{1, 2}「差」をマイナス記号で表すのは通常の計算と同じです。さらにdifferenceメソッドでも同じ事ができます。
c = a.difference(b)対象差集合
最後に対象差集合です。対象差集合はちょうど積集合の逆になります。

2つの集合があり、これまでと同様、2つの集合には共通している部分があるとします。
この重なり合った部分は、AにもBにも含まれる値です。これを抜き出すのが差集合でしたが、対象差集合はこの逆。AかBどちらかにしか含まれない値だけを抜き出して、新たな集合を作り出します。
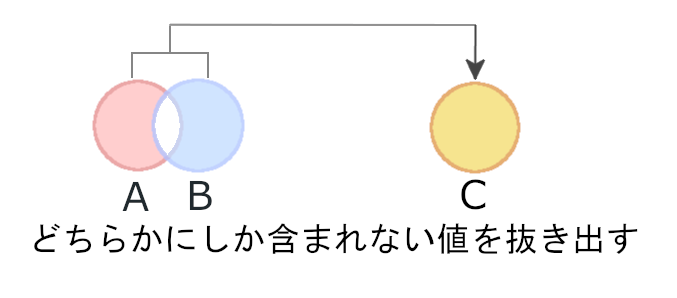
これもPythonでやってみましょう。
a = {1,2,3,4,5}
b = {3,4,5,6,7}
c = a ^ b
print(c) #{1, 2, 6, 7}対象差集合には「^」(キャレット記号)を演算子として使用します。
こちらもメソッドが用意されています。symmetric_differenceメソッドです。
c = a.symmetric_difference(b)